Albert Einstein announces the next Cape Cod Astronomical Society meeting at Werner Schmidt Observatory. (astro humor)
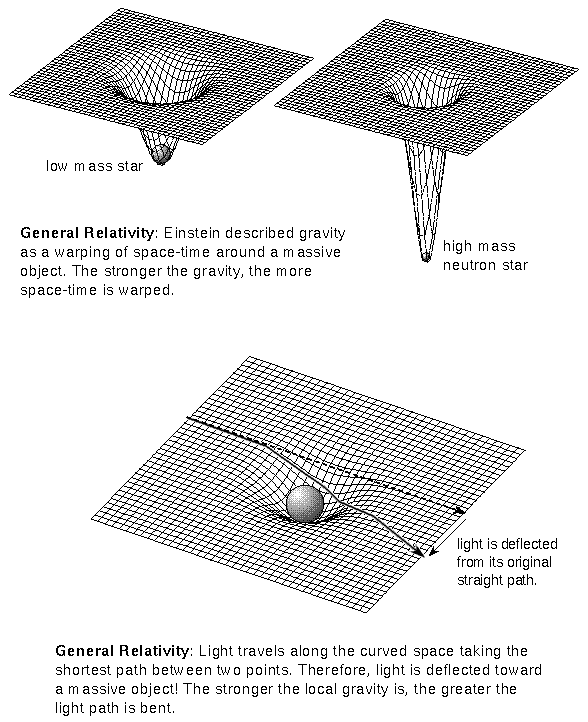
Gravitational Time Dilation
Einstein's Special Theory of Relativity predicted that time does not flow at a fixed rate: moving clocks appear to tick more slowly relative to their stationary counterparts. But this effect only becomes really significant at very high velocities that app roach the speed of light.
When "generalized" to include gravitation, the equations of relativity predict that gravity, or the curvature of spacetime by matter, not only stretches or shrinks distances (depending on their direction with respect to the gravitational field) but also w ill appear to slow down or "dilate" the flow of time.
In most circumstances in the universe, such time dilation is miniscule, but it can become very significant when spacetime is curved by a massive object such as a black hole. For example, an observer far from a black hole would observe time passing extremely slowly for an astronaut falling through the hole's boundary. In fact, the distant observer would never see the hapless victim actually fall in. His or her time, as measured by the observer, would appear to stand still. The slowing of time near a very simple black hole has been simulated on supercomputers at NCSA and visualized in a computer-generated animation.
